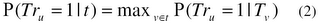Sunday, July 23, 2006
#8 (from RTE 1) Summary
- Probabilistic approach
- They do lexical entailment based on web co-occurrence statistics in a bag of words representation.
- It does not rely on syntactic or other deeper analysis.
Suppose:
h1 = "Harry was born in Iowa.",
t1 includes "Harry's birthplace is Iowa.", and
t2 includes "Harry is returning to his Iowa hometown to get married."
P(h1 is TRUE | t1) ought to be much higher than P(h1 is TRUE | t2).
More specifically, we might say that the probability p of h1 being true should be estimated based on the percentage of cases in which someone's reported hometown is indeed his/her birthplace. And t2 would not be accepted as a definite assessment for the truth of h1.
However, in the absence of other definite information, t2 may partly satisfy the information
need for an assessment of the probable truth of h1, with p providing a confidence probability for this inference.
A Probabilistic Setting
Let t denote a possible text, and
let h denote a possible hypothesis.
t is in T (space of possible texts)
h is in H(space of all possible hypothesis)
let source be the thing that generates text t.
Meanings are captured by hypothesis and their truth values.
A hypothesis h in H is a propositional statement that can be assigned a truth value.
a possible world is:
from (1) and (2), the entailment probability is estimated as:
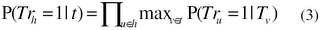
Web-based Estimation of P(Tr_u = 1 | T_v):
Given that the possible world of the text is not observed we do not know the truth assignments of hypotheses for the observed texts. We therefore further make the simplest assumption that all hypotheses stated verbatim in a document are true and all others are false and hence:
P(Tr_u = 1 | T_v) = P(T_u | T_v) = lep (u, v)
[lep: lexical entialment probability]
lep is estimated based on maximum likelihood counts:
lep(u,v) is proportional to (n_uv / n_v)
[n_v: number of documents containing v,
n_uv: number of documents containing both u and v]
If this value is greater than a empirically tuned threshold k, the entailment holds.
accuracy = 59%
cws = 0.57
- They do lexical entailment based on web co-occurrence statistics in a bag of words representation.
- It does not rely on syntactic or other deeper analysis.
Suppose:
h1 = "Harry was born in Iowa.",
t1 includes "Harry's birthplace is Iowa.", and
t2 includes "Harry is returning to his Iowa hometown to get married."
P(h1 is TRUE | t1) ought to be much higher than P(h1 is TRUE | t2).
More specifically, we might say that the probability p of h1 being true should be estimated based on the percentage of cases in which someone's reported hometown is indeed his/her birthplace. And t2 would not be accepted as a definite assessment for the truth of h1.
However, in the absence of other definite information, t2 may partly satisfy the information
need for an assessment of the probable truth of h1, with p providing a confidence probability for this inference.
A Probabilistic Setting
Let t denote a possible text, and
let h denote a possible hypothesis.
t is in T (space of possible texts)
h is in H(space of all possible hypothesis)
let source be the thing that generates text t.
Meanings are captured by hypothesis and their truth values.
A hypothesis h in H is a propositional statement that can be assigned a truth value.
a possible world is:
w: H -> {0:false, 1:true}
It represents the set of w's concrete truth value assignments for all possible propositions.
Whenever the source generates a text t, it generates also hidden truth assignments that constitute a possible world w. (The hidden w is perceived as a "snapshot" of the (complete) state of affairs in the world within which t was generated.)
The probability distribution of the source, over all possible texts and truth assignments T × W, is assumed to reflect only inferences that are based on the generated texts.
That is, it is assumed that the distribution of truth assignments is not bound to reflect the state of affairs in any "real" world, but only the inferences about propositions' truth that are related to the text.
In particular, the probability for generating a true hypothesis h that is not related at all to the corresponding text is determined by some prior probability P(h), which is not bound to reflect h's prior in the "real" world.
EX:
h="Paris is the capital of France" might well be false when the generated text is not related at all to Paris.
1) For a hypothesis h, we denote as Tr_h the random variable whose value is the truth value assigned to h in the world of the generated text. Correspondingly, Tr_h=1 is the event of h being assigned a truth value of 1 (True).
2) For a text t, we use t to denote also the event that the generated text is t (as usual, it is clear from the context whether t denotes the text or the corresponding event).
We say that t probabilistically entails h (denoted as t->h) if t increases the likelihood of h being true, that is, if P(Tr_h = 1| t) > P(Tr_h = 1)
The probabilistic confidence value corresponds to P(Tr_h = 1| t).
We assume that the meanings of the individual (content) words in a hypothesis h={u_1, …, u_m} can be assigned truth values. We only assume that truth values are defined for lexical items, but do not explicitly annotate or evaluate this sub-task.
Given this setting, a hypothesis is assumed to be true if and only if all its lexical components are
Whenever the source generates a text t, it generates also hidden truth assignments that constitute a possible world w. (The hidden w is perceived as a "snapshot" of the (complete) state of affairs in the world within which t was generated.)
The probability distribution of the source, over all possible texts and truth assignments T × W, is assumed to reflect only inferences that are based on the generated texts.
That is, it is assumed that the distribution of truth assignments is not bound to reflect the state of affairs in any "real" world, but only the inferences about propositions' truth that are related to the text.
In particular, the probability for generating a true hypothesis h that is not related at all to the corresponding text is determined by some prior probability P(h), which is not bound to reflect h's prior in the "real" world.
EX:
h="Paris is the capital of France" might well be false when the generated text is not related at all to Paris.
1) For a hypothesis h, we denote as Tr_h the random variable whose value is the truth value assigned to h in the world of the generated text. Correspondingly, Tr_h=1 is the event of h being assigned a truth value of 1 (True).
2) For a text t, we use t to denote also the event that the generated text is t (as usual, it is clear from the context whether t denotes the text or the corresponding event).
We say that t probabilistically entails h (denoted as t->h) if t increases the likelihood of h being true, that is, if P(Tr_h = 1| t) > P(Tr_h = 1)
The probabilistic confidence value corresponds to P(Tr_h = 1| t).
We assume that the meanings of the individual (content) words in a hypothesis h={u_1, …, u_m} can be assigned truth values. We only assume that truth values are defined for lexical items, but do not explicitly annotate or evaluate this sub-task.
Given this setting, a hypothesis is assumed to be true if and only if all its lexical components are
true.
We assume that the truth probability of a term in a hypothesis h is independent of the truth of the other terms in h:
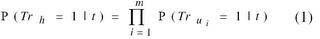
We assume that the truth probability of a term in a hypothesis h is independent of the truth of the other terms in h:
For a given word u, to estimate P(Tr_u = 1 | t), where t = {v_1, ..., v_n}, we further assume that the majority of the probability mass comes from a specific entailing word in t:
where T_v denotes the event that a generated text contains the words v.
where T_v denotes the event that a generated text contains the words v.
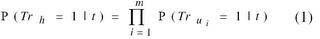
from (1) and (2), the entailment probability is estimated as:
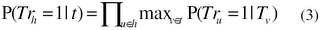
Web-based Estimation of P(Tr_u = 1 | T_v):
Given that the possible world of the text is not observed we do not know the truth assignments of hypotheses for the observed texts. We therefore further make the simplest assumption that all hypotheses stated verbatim in a document are true and all others are false and hence:
P(Tr_u = 1 | T_v) = P(T_u | T_v) = lep (u, v)
[lep: lexical entialment probability]
lep is estimated based on maximum likelihood counts:
lep(u,v) is proportional to (n_uv / n_v)
[n_v: number of documents containing v,
n_uv: number of documents containing both u and v]
If this value is greater than a empirically tuned threshold k, the entailment holds.
accuracy = 59%
cws = 0.57
# posted by Bengi Mizrahi @ 1:54 PM 
